Teoria da informação e entropia – como passamos do conhecimento para a informação?

Publicado em por

O que é entropia nos termos da física?

Dente de leão simbolizando a entropia. Créditos: www.pngwing.com.

Entropia (do grego εντροπία, entropia), unidade [J/K] (joules por kelvin), é uma grandeza termodinâmica que mede o grau de liberdade molecular de um sistema, está associado ao seu número de configurações (ou microestados), ou seja, de quantas maneiras as partículas (átomos, íons ou moléculas) são distribuídos em níveis energéticos quantizados, incluindo translacionais, vibracionais, rotacionais e eletrônicos. Entropia também é geralmente associada à aleatoriedade, dispersão de matéria e energia, e “desordem” (não em senso comum) de um sistema termodinâmico. A entropia é a entidade física que rege a segunda lei da termodinâmica, à qual estabelece que a ela deve aumentar para processos espontâneos e em sistemas isolados. Para sistemas abertos, deve-se estabelecer que a entropia do universo (sistema e suas vizinhanças) deve aumentar devido ao processo espontâneo até o meio formado por sistema + vizinhanças atingir um valor máximo no estado de equilíbrio. Neste ponto, é importante ressaltar que vizinhanças se entende como a parte do resto do universo capaz de interagir com o sistema, através de, por exemplo: trocas de calor.

Função da entropia binária, ensaio de Bernoulli, princípio da entropia máxima. Créditos: http://www.pngwing.com.

A distribuição de Bernoulli, nome em homenagem ao cientista suíço Jakob Bernoulli, é a distribuição discreta do espaço amostral {0, 1}, que tem valor 1 com a probabilidade de sucesso p e valor 0 com a probabilidade de falha q = 1 − p.

Resumo:

  • P(1) = p
  • P(2) = q
  • p + q = 1
  • q = 1 − p

Se X é uma variável aleatória com essa distribuição, teremos:

P(X=1)=1-P(X=0)=1-q=p

Um exemplo clássico de uma experiência de Bernoulli é uma jogada única de uma moeda. A moeda pode dar “coroa” com probabilidade p ou “cara” com probabilidade 1 − p. A experiência é dita justa se p = 0.5, indicando a origem dessa terminologia em jogos de apostas (a aposta é justa se ambos os possíveis resultados têm a mesma probabilidade).

Gelo derretendo. (C) WiKi.

Uma definição formal de entropia em termos de possibilidade é: entropia é uma medida aditiva do número de possibilidades disponíveis para um sistema. Assim, a entropia de um sistema físico é uma medida aditiva do número de microestados possíveis que podem ser realizados pelo sistema. E a entropia de uma fonte de mensagem é uma medida aditiva do número de mensagens possíveis que podem ser escolhidas dessa fonte de mensagens.

Obs.: com a morte de um organismo vivo, a entropia do organismo aumenta. À medida que o interior morre, seus restos são espalhados pelo vento. No entanto, mesmo nesta morte, novas possibilidades são distribuídas.

Entropia na teoria da informação

A falta de informação é uma medida da informação necessária para escolher um microestado específico de um conjunto de microestados possíveis ou uma mensagem de uma fonte de mensagens possíveis. Ao passo que a incerteza pode ser entendida como a falta de informação sobre uma questão de interesse para um determinado agente (por exemplo, um tomador de decisão humano ou uma máquina), uma condição de conhecimento limitado em que é impossível descrever exatamente o estado do mundo ou sua evolução futura. Portanto, podemos representar essa origem como:

μ(∅) = 0

O significado dessa fórmula é: a entropia do vazio ∅ (origem do conhecimento) é zero 0.

A teoria da informação lógica cumpre precisamente a máxima de Kolmogorov. Ele começa simplesmente com um conjunto de distinções definidas por uma partição (divisão) em um conjunto finito U, onde uma distinção é um par ordenado de elementos de U em blocos distintos da partição – podemos representar isso como Probabilidade/Subespaços. Assim, o objeto “combinatório finito” é o conjunto de distinções (“distset”) ou conjunto de informações (“infoset”) associado à partição – Informação/Partição; ou seja, o complemento em U × U da relação de equivalência associada à partição. Para obter uma medida quantitativa de informação, qualquer distribuição de probabilidade em U define uma medida de probabilidade do produto de U × U, e a entropia lógica é simplesmente essa medida de probabilidade no conjunto de informações. Esta descrição motivacional da teoria da informação lógica será agora desenvolvida em detalhes.

O conceito de incerteza desempenha um papel semelhante. Quanto maior e mais variado o conjunto a partir do qual um sistema pode ser escolhido e quanto maior e mais variada a fonte da mensagem da qual uma mensagem pode ser extraída, mais incerto será o resultado e mais alta será a entropia. A entropia lógica é a medida (no sentido técnico não negativo da teoria da medida) de informações que surgem da lógica de partição assim como a teoria da probabilidade lógica surge da lógica de subconjuntos (subespaços).

Entropia de Shannon

Representação da origem do conhecimento c(∅) com o particionamento binário proposto por Shannon. Créditos imagem: CC {rcristo.com.br}

Consequentemente, a entropia de Shannon é interpretada como o número médio do limite de bits necessários por mensagem. Em termos de distinções, este é o número médio de partições binárias necessárias para distinguir as mensagens.

Podemos representar a entropia de Shannon pela fórmula:

H(p)=\sum_{k=1}^{m} p_{k} \log _{2}\left(\frac{1}{p_{k}}\right)

Considere uma árvore binária de três níveis, onde cada ramo se divide em dois ramos equiprováveis em cada nível, como em 2^{3}=8, folhas são as mensagens, cada uma com probabilidade \frac{1}{8}. Uma entropia multiplicativa de Shannon é o número de mensagens equiprováveis 2^{3}=8, e a entropia de Shannon é o número de decisões binárias ou bits \log \left(2^{3}\right)=3 necessários para determinar cada mensagem que, neste exemplo canônico, é o comprimento do código binário de cada mensagem.

Máquina de Galton

Tabuleiro de Galton em movimento. Créditos Wikipédia.

Se pensarmos na árvore como uma máquina de Galton com bolinhas de gude caindo da raiz e tomando um dos galhos com igual probabilidade, então a probabilidade de alcançar qualquer folha em particular é, obviamente, \frac{1}{8}. A entropia lógica é a probabilidade de que em duas tentativas diferentes a bola de gude alcance folhas diferentes.

h (p) = 1 − 8 × \left(\frac{1}{8}\right)^{2}=1-\frac{1}{8}=\frac{7}{8}

Entropia como possibilidade é uma palavra adequada e, ao contrário da incerteza e da falta de informação, tem conotação positiva. Assim, de acordo com a segunda lei da termodinâmica, um sistema termodinâmico isolado sempre evolui no sentido de abrir novas possibilidades. E quanto maior o conjunto de possibilidades a partir do qual um microestado ou uma mensagem podem ser realizados ou escolhidos, maior será a entropia do sistema físico ou a entropia de Shannon da fonte da mensagem.

Convenções sobre operações indexadas no conjunto vazio

  • Somas vazias = 0
  • Produtos vazios = 1
  • Uniões vazias = ∅
  • Interseções vazias = o conjunto universo
  • Permutações vazias = 1

O conjunto vazio { } = ∅ determina a origem dos microestados ou da informação que será medida.

{RC}.

A medida direta é a entropia lógica que é a medida quantitativa das distinções feitas por uma partição. A entropia de Shannon é uma transformação ou reunificação da entropia lógica para a teoria matemática das comunicações. O matemático Andrei Kolmogorov sugeriu que as informações devem ser definidas independentemente da probabilidade, de modo que a entropia lógica é definida pela primeira vez em termos do conjunto de distinções de uma partição e, em seguida, uma medida de probabilidade no conjunto define a versão quantitativa da entropia lógica.

A entropia de Shannon é frequentemente apresentada como sendo a mesma que a entropia de Boltzmann.

Conectividade espacial e subespacial

Trabalhamos com um espaço métrico que entendemos como um plano complexo, a menos que especificado de outra forma. A letra Ω denotará um conjunto aberto no espaço métrico, consequentemente, uma região é simplesmente conectada se e somente se seu complemento no plano complexo estendido estiver conectado. Assim, uma região é simplesmente conectada se e somente se não tiver orifícios. Este é um critério muito transparente para determinar se uma região está simplesmente conectada ou não.

Para qualquer conjunto finito U, uma medida μ (lê-se: mi é a décima segunda letra do alfabeto grego) é uma função μ: ℘ (U) → R tal que:

μ(∅) = 0,

para qualquer E ⊆ U, μ (E) ≥ 0, e

para quaisquer subconjuntos disjuntos E1 e E2, μ (E1 ∪ E2) = μ (E1) μ (E2).

Seja X um espaço métrico e E ⊆ X, começamos com uma definição de conectividade

Definição: um conjunto E é conectado se E não puder ser escrito como uma união disjunta de dois subconjuntos abertos relativos não vazios de E. Assim, E = A ∪ B com A ∩ B = ∅ e A, B aberto em E implica que A = ∅ ou B = ∅. Caso contrário, E = A ∪ B é chamado de separação E em conjuntos abertos. Por exemplo, a união E de dois discos abertos separados A e B não está conectada, pois:

E = A ∪ B = (A ∪ B) ∩ E = (A ∩ E) ∪ (B ∩ E)

onde A ∩ E e B ∩ E não estão vazios, disjuntos e relativamente abertos em E. Como em C, um conjunto conectado aberto em um espaço métrico é chamado de região.

Definição: um subconjunto máximo conectado de E é chamado de componente de E. Para a ∈ E, seja C(a) a união de todos os subconjuntos conectados de E contendo a. Observamos que a ∈ C (a) uma vez que {a} está conectado e:

E=\bigcup_{a \in E} C(a)

Fornecemos algumas propriedades de C(a).

(i) C(a) está conectado.

A prova é por contradição. Seja C(a) = A ∪ B uma separação de C(a) em conjuntos abertos. Podemos assumir que a ∈ A e b ∈ B. Então, como b ∈ C(a) e C(a) é a união de todos os subconjuntos conectados de E contendo a, existe E0 ⊆ E tal que E0 ⊆ C(a) está conectado e a ∈ E0, b ∈ E0. Por isso:

E0 = E0 ∩ C (a) = E0 ∩ (A ∪ B) = (E0 ∩ A) ∪ (E0 ∩ B)

implica que ou E0 ∩ A = ∅ ou E0 ∩ B = ∅. Isso é uma contradição, pois a ∈ E0 ∩ A e b ∈ E0 ∩ B.

Assim, cada componente de E tem a forma C(a) com um ∈ E.

Os componentes de E são disjuntos ou idênticos.

Seja a, b ∈ E. Suponha que C(a) ∩ C(b) = ∅. Então provamos que C(a) = C(b). Seja x ∈ C(a) ∩ C(b). Então x ∈ C(a). Como C(a) está conectado, deduzimos que C(a) ⊆ C(x). Então a ∈ C(x) que implica C(x) ⊆ C(a) já que C(x) está conectado. Assim, C(a) = C(x). Da mesma forma C(b) = C(x) e, portanto, C(a) = C(b).

Os componentes de um conjunto aberto são abertos

Seja E um conjunto aberto. Basta mostrar que C(a) com a ∈ E está aberto. Seja x ∈ C(a).

(ii) Então C(x) = C(a).

Como x ∈ E e E é aberto, existe r > 0 tal que D(x, r) ⊆ E. De fato, D(x, r) ⊆ C (x) já que D(x, r) está conectado contendo x. Assim, x ∈ D(x, r) ⊆ C(a) e, portanto, C(a) é aberto.

Ao combinar (i), (ii) concluímos: um conjunto aberto em um espaço métrico é uma união disjunta de regiões.

Para os pontos P0, P1, …, Ps no plano complexo, escrevemos [P0, P1, …, Ps] para o caminho poligonal obtido unindo P0 a P1, P1 a P2, …, Ps− 1 a Ps por segmentos de linha. Agora fornecemos um critério fácil de aplicar para mostrar que os conjuntos no plano estão conectados.

Seja E um subconjunto aberto não vazio de C. Então E é conectado se e somente se quaisquer dois pontos em E podem ser unidos por um caminho poligonal que está em E.

Prova: Suponha que E está conectado. Como E = ∅, seja a ∈ E. Seja E1 o subconjunto de todos os elementos de E que podem ser unidos a a por um caminho poligonal. Seja E2 o complemento de E1 em E. Então:

E = E1 ∪ E2 com E1 ∩ E2 = ∅, a ∈ E1.

É suficiente mostrar que E1 e E2 são subconjuntos abertos de E. Então E2 = ∅ visto que E está conectado e a ∈ E1. Assim, cada ponto de E pode ser unido a a por um caminho poligonal que fica em E. Portanto, quaisquer dois pontos de E podem ser unidos por um caminho poligonal que fica em E via a.

Primeiro, mostramos que E1 está aberto. Seja a1 ∈ E1. Então a1 ∈ E e como E está aberto, encontramos r1 > 0 tal que D(a1, r1) ⊆ E. Qualquer ponto de D(a1, r1) pode ser unido a a1 e, portanto, a a por um caminho poligonal que fica em E desde a1 ∈ E1. Assim, a1 ∈ D(a1, r1) ⊆ E1. A seguir, mostramos que o E2 está aberto. Seja a2 ∈ E2. Novamente encontramos r2 > 0 de modo que D(a2, r2) ⊆ E visto que E está aberto. Agora, como acima, vemos que nenhum ponto deste disco pode ser unido a a como a2 ∈ E2 e, portanto, a2 ∈ D(a2, r2) ⊆ E2. Agora assumimos que se quaisquer dois pontos de E podem ser unidos por um caminho poligonal em E, mostramos que E está conectado. Deixe:

E = E1 ∪ E2

Seja uma separação de E em conjuntos abertos. Não há perda de generalidade em assumir que existem pontos a1 ∈ E1 e a2 ∈ E2 tais que:

χ (t) = ta1 (1 – t) a2 com 0 <t <1

é um segmento aberto de a2 a a1 situado em E. Deixe:

V = {t ∈ (0, 1)|χ(t) ∈ E1} e W = {t ∈ (0, 1)|χ(t) ∈ E2}.

Vimos que V e W estão abertos em (0, 1). Além disso, temos a separação do intervalo aberto (0, 1) em conjuntos abertos (0, 1) = V ∪ W, V ∩ W = ∅

Como a1 ∈ E1 e E1 está aberto, existe r3 > 0 com D(a1, r3) ⊆ E1. Isso implica V = ∅. Da mesma forma W = ∅. Portanto, o intervalo (0, 1) não está conectado. Isso é uma contradição.

Partições Young

Para uma partição λ, o diagrama de Young Yλ da forma λ é um diagrama justificado à esquerda |λ| em caixas, com λi caixas pretas na i-ésima coluna, denotamos o conjunto de todos os diagramas Young contidos em um k × (m − k) caixa por Tk,m−k \mathcal{T}_{m}=\cup_{k=0}^{m}

Por exemplo, os diagramas de Young no conjunto T2,2 são dados por:

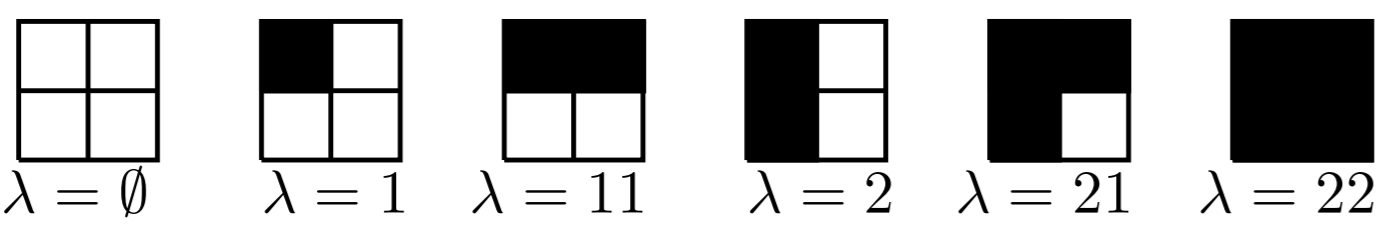
O conjunto T3 é dado por:

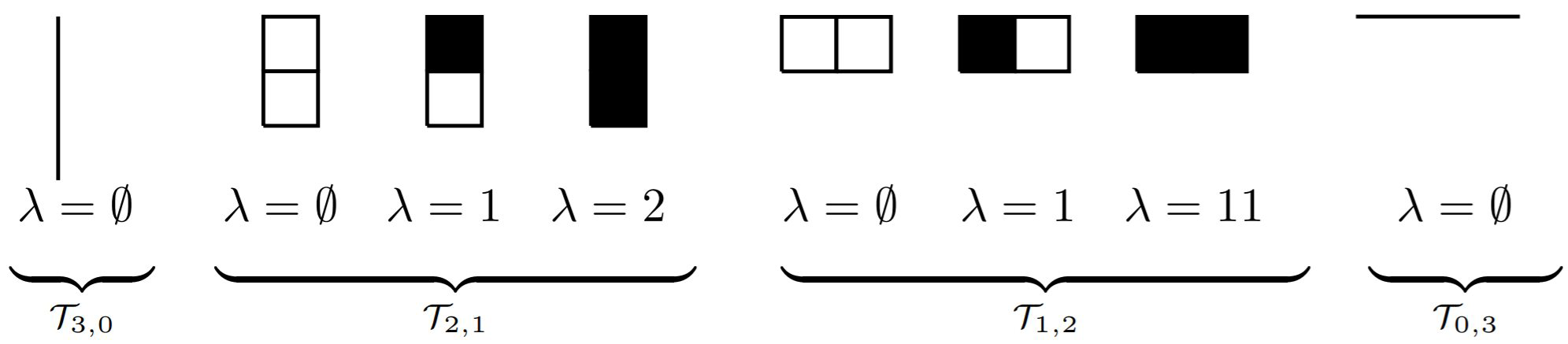
Observe que cada diagrama de Young em Tm pode ser obtido de um diagrama de Young em Tm−1 adicionando uma coluna vazia à sua direita ou uma linha preenchida antes de sua primeira linha. Por exemplo, as partições obtidas da partição λ = ∅ ∈ T1,2 são dadas por 1 ∈ T2,2 e ∅ ∈ T1,3. Assim, o número de diagramas de Young no conjunto Tm é dado por 2m. A seguir, identificamos uma partição e seu diagrama Young associado.

Para qualquer partição λ = λ1 ··· λk, definimos λ∗ como a partição λ∗ = (λ1 + 1)(λ2 + 1)··· (λk + 1) e λ∗ como a partição λ∗ = λ1 ·· · λk0.

Em outras palavras, λ ∗ é o diagrama de Young que é obtido de λ adicionando uma linha preenchida antes da primeira linha de λ, e λ ∗ é o diagrama de Young que é obtido de λ adicionando uma coluna vazia no lado direito de λ.

Entropia estatística

Em 1877, Ludwig Boltzmann visualizou um método probabilístico para medir a entropia de um determinado número de partículas de um gás ideal, na qual ele definiu entropia como proporcional ao logaritmo neperiano do número de microestados que um gás pode ocupar.

S=k \cdot \ln \Omega

Onde S é a entropia, k é a constante de Boltzmann e Ω é o número de microestados possíveis para o sistema.

Resolução da fórmula para um sistema moeda com 2 microestados

A probabilidade é uma medida que descreve a chance de um determinado evento ocorrer. Ela varia entre ∅ (evento impossível) e 1 (evento certo). Quando temos um sistema físico, a entropia é uma medida da quantidade de desordem ou incerteza presente nesse sistema. Quanto maior a entropia, maior é a incerteza ou desordem.

A fórmula de Boltzmann relaciona a entropia (S) de um sistema com a probabilidade (Ω) de encontrar esse sistema em um determinado estado. Essa fórmula é dada por:

S = k ln Ω

Onde:

  • S é a entropia do sistema.
  • k é a constante de Boltzmann, que relaciona a temperatura termodinâmica com a energia térmica do sistema. Seu valor é aproximadamente 1,380.649 × 10^-23 J/K (joules por kelvin).
  • Ω é o número de microestados possíveis do sistema.

Para entender melhor essa fórmula, vamos considerar um exemplo com uma moeda. Suponha que temos uma moeda não viciada, ou seja, com cara (C) e coroa (K) tendo igual probabilidade de ocorrer. O número total de microestados possíveis é 2, pois há 2 resultados possíveis: C ou K.

A probabilidade de obter cara ou coroa é 1/2 para cada resultado. Portanto, Ω = 2 e ln Ω ≈ ln 2 ≈ 0,693.

Agora, usando a fórmula de Boltzmann, podemos calcular a entropia do sistema:

S = k ln Ω ≈ (1,380.649 × 10^-23 J/K) * 0,693 ≈ 9,57 × 10^-24 J/K

Isso nos dá a medida da entropia do sistema da moeda.

A fórmula de Boltzmann é amplamente utilizada na termodinâmica estatística para relacionar a entropia de um sistema com a probabilidade de seus microestados. Ela desempenha um papel fundamental na compreensão de fenômenos como a distribuição de energia térmica em sistemas e a descrição estatística de partículas em equilíbrio.

O trabalho de Boltzmann consistiu em encontrar uma forma de obter a equação entrópica fundamental S a partir de um tratamento matemático-probabilístico, facilmente aplicável aos sistemas em questão. Ao fazê-lo, conectou o todo poderoso formalismo termodinâmico associado à equação fundamental a um método de tratamento probabilístico simples que exige apenas considerações físicas primárias sobre o sistema em análise, obtendo, a partir de considerações básicas, todo o comportamento termodinâmico do sistema.

Como chegamos ao bit de informação

A fim de entender de forma intuitiva o que significa dizer 1 bit de informação, imagine a seguinte situação, um viajante, decide sair de sua cidade, no ponto marcado com a letra “A” na figura abaixo e chegar ao seu destino no ponto “D”.

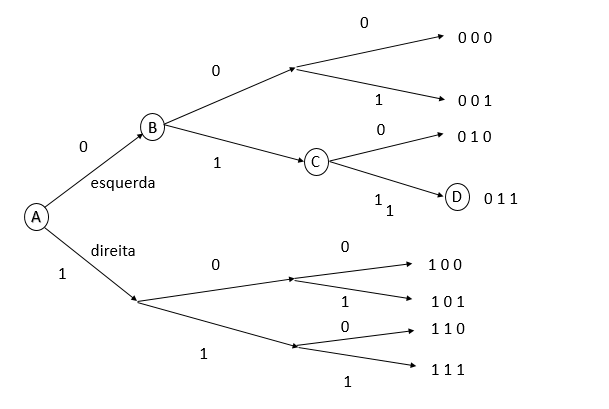
8 destinos =2^{3} destinos. Créditos Wikipédia.

O caminho entre “A” e “D” possui várias bifurcações (como os pontos “B” e “C”). Assumindo que o viajante desconhece o caminho, em cada cidade que passar (representada pelas bifurcações) ele pede uma informação, perguntando se deve seguir à direita ou à esquerda. Na figura anterior, dizer que ele deve seguir à esquerda é o mesmo que mostrar o dígito binário 0 a ele, e um sinal de que deve seguir à direita o mesmo que mostrar o dígito 1.

Dessa forma, como é possível ver pela figura, ele terá que pedir informação nos pontos “A”, “B” e “C”. Note que independente do destino {000, 001, 011, . . .} o número de perguntas para alcançá-lo (neste caso) é sempre três. Ou seja, escolher entre oito destinos requer três perguntas:

8 destinos equivale a 2^{3} destinos

Note que o expoente do número dois na equação anterior é igual ao número de perguntas feitas. Define-se então que para escolher entre um dos oito possíveis destinos é necessária uma quantidade de informação igual a 3 bits.

Aplicando o logaritmo de base dois na expressão anterior, temos:

3=\log _{2} 8 \quad[bits]

É importante salientar que como o viajante poderia igualmente ter escolhido qualquer um dos destinos finais possíveis eles são todos equiprováveis com probabilidade p = 1/8.

De forma análoga, para o caso em que se tem m possíveis destinos, e supondo que o viajante possa escolher qualquer um deles com igual probabilidade, a quantidade de informação, em bits, para alcançar um dos possíveis destinos é dada pela relação a seguir:

n=\log _{2} 2=1 bits

Informação de Shannon (h) ou surpresa

Usarei de outro exemplo para explicar a medida de Informação de Shannon h ou surpresa. Imagine nesse caso, uma moeda desonesta (enviesada), que tem probabilidade p_{\text {cara }}=0.9 de dar cara e probabilidade p_{\text {coroa }}=0.1 de dar coroa.

Por você estar acostumado com a jogada dessa moeda quase sempre dê cara, esse resultado não te surpreende. Mas um resultado coroa te surpreende por conta da “raridade” do evento.  Pensando nisso, uma forma natural de se definir essa surpresa, seria como algo proporcional ao inverso da probabilidade p de ocorrência do evento, deste modo quanto menor essa probabilidade maior a surpresa.

Shannon definiu essa grandeza como:

h=\log _{2} \frac{1}{p}

Utilizando o logaritmo na base dois mantêm-se a propriedade de aditividade dessa grandeza. Dessa maneira podemos calcular a surpresa da jogada da moeda retornar cara \left(h_{\text {cara }}\right) ou coroa \left(h_{\text {coroa }}\right) de acordo com a definição anterior.

h_{\text {cara }}=\log _{2} \frac{1}{0.9}=0.152

e,

h_{\text {coroa }}=\log _{2} \frac{1}{0.1}=3.322

De fato, \left(h_{\text {cara }}\right) > \left(h_{\text {coroa }}\right), que surpresa!

A fim de chegar na formulação matemática da entropia, imagine por exemplo uma variável aleatória X, que pode assumir dois valores distintos x1 e x2 com probabilidades p1 e p2, respectivamente. Seguindo a notação definida na seção.

Variáveis aleatórias discretas, temos:

X = {x1, x2}

p(X) = {p1, p2}

A informação de Shannon associada a cada um dos valores é:

h1=\log _{2} \frac{1}{p1}

e,

h2=\log _{2} \frac{1}{p2}

Na prática, geralmente nós não estamos interessados em saber a surpresa de um valor em particular que uma variável aleatória pode assumir, e sim a surpresa associada com todos os possíveis valores que essa variável aleatória pode ter. De modo a obtermos a surpresa associada a todos possíveis valores que X pode assumir, define-se a entropia H(X) como a informação média de Shannon:

H(X)=p_{1} h_{1}+p_{2} h_{2}=p_{1} \log _{2} \frac{1}{p_{1}}+p_{2} \log _{2} \frac{1}{p_{2}}=\sum_{i=1}^{2} p_{i} \log _{2} \frac{1}{p_{i}}

Caso X, possa assumir m valores, a expressão anterior pode ser escrita de um modo resumido:

H(X)=-\sum_{i=1}^{m} p_{i} \log _{2} p_{i}

A entropia do dado de seis faces

Uma aplicação direta para a equação da entropia definida anteriormente pode ser obtida como exemplo de um dado de seis faces. Representando o dado pela variável aleatória X, temos:

X=\{1,2,3,4,5,6\}

e,

p(X)=\{1 / 6,1 / 6,1 / 6,1 / 6,1 / 6,1 / 6\}

Desse modo a entropia contém:

H(X)=-\sum_{i=1}^{6} p_{i} \log _{2} p_{i}=-6 \frac{1}{6} \log _{2} \frac{1}{6}=2.585 bits

Moeda boa, moeda ruim

Considere a moeda honesta, representada pela variável aleatória M_{1}

M_{1}=\{cara, coroa \}=\{0,1\}

e,

p\left(M_{1}\right)=\left\{p_{\text {cara }}=0.5, p_{\text {coroa }}=0.5\right\}

E a moeda enviesada, como aquela utilizada para exemplificar a informação de Shannon, representada pela variável aleatória M_{2}.

M_{2}=\{cara, coroa \}=\{0,1\}

e,

p\left(M_{2}\right)=\left\{p_{\text {cara }}=0.9, p_{\text {coroa }}=0.1\right\}

Note que um resultado cara é representado pelo dígito 0 e um resultado coroa por um dígito 1. A entropia de cada uma das moedas pode ser calculada então:

H\left(M_{1}\right)=-\sum_{i=1}^{2} p_{i} \log _{2} p_{i}=-2 \frac{1}{2} \log _{2} \frac{1}{2}=1 bit

e,

H\left(M_{2}\right)=-\sum_{i=1}^{2} p_{i} \log _{2} p_{i}=-(0.9 \log _{2}0.9+0.1\log _{2}0.1)=0.469 bits

Neste caso a entropia da moeda honesta é maior do que a da moeda desonesta, pois há uma incerteza maior em relação ao resultado de cada lançamento.

Uma regra simples na teoria da informação é que um bit de informação é equivalente a cortar as possibilidades pela metade, porque metade das possibilidades seria equivalente a um evento com probabilidade p=\frac{1}{2} e este contém \log _2 \frac{1}{\frac{1}{2}}=\log _2 2=1 \text { bit } de informação.

O segredo da teoria da informação são as inteligentes escolhas matemáticas que Claude Shannon fez ao definir a informação. A informação é alta quando as probabilidades são baixas, e a informação é somada quando os resultados são independentes.

O que são dados?

O significado de dados é: um conjunto de informações que depende da forma (espacial ou subespacial – codificado em computadores) e do tipo (estruturados ou não estruturados). Ex: uma letra, palavra, imagem, vídeo, símbolos matemáticos, uma página de texto, um livro em formato pdf, um livro em papel, uma planilha, um formulário em papel ou online, etc. Os dados podem ser classificados no tipo: estruturados e não estruturados.

Representação e codificação de dados nos computadores

Os computadores foram inventados para trabalhar com a informação na forma de dados, seguindo uma série de critérios lógicos que determinam o tratamento da informação (codificação), representação, armazenamento, recuperação e transmissão. Os critérios básicos são:

  • Dado = informação potencialmente valiosa
  • Informação = conhecimento adquirido através da interpretação dos dados

{RC} Perguntou à IA GPT?

Podemos afirmar que, em um contexto geral, um dado pode ser considerado como uma forma de informação armazenada. Os dados são elementos brutos, como fatos, números ou símbolos, que podem ser coletados, armazenados e processados. No entanto, é importante destacar que a informação vai além dos dados brutos.

A informação é a interpretação ou aquisição de conhecimento a partir dos dados. Ela envolve o processamento, análise e compreensão dos dados, atribuindo-lhes significado e contexto. A informação resulta da organização e estruturação dos dados, permitindo que sejam utilizados para tomar decisões, tirar conclusões ou gerar novos conhecimentos.

Portanto, podemos dizer que os dados são a matéria-prima, enquanto a informação é o produto resultante da interpretação e compreensão dos dados. A informação é o resultado da aquisição de conhecimento a partir dos dados disponíveis. 😉

Formas representativas e codificação

Ex: O UTF-8 é uma série unicode.

Representação da codificação vazia (null)

Como pode ser visto na figura abaixo, a codificação vazia é o primeiro critério codificado pela tabela ASCII, não poderia ser diferente, pois é a origem da codificação.

Em todos os computadores a codificação base começa com vazio, pois essa é a origem da informação, e não poderia ficar de fora. Clique na imagem para ver a tabela toda. Ex: clique em qualquer campo de formulário ou busca, segure a tecla ALT em seu computador pessoal e digite no teclado ao lado: 155, obterá o símbolo de vazio ø minúsculo, para vazio maiúsculo, pressione ALT 157, Ø.

Obs.: um livro em papel é um dado espacial, um livro em PDF ou EPUB é um dado subespacial (codificado em computadores).

O principal objetivo das minhas pesquisas é esclarecer você leitor para que se proteja dos absurdos conceituais que os influenciadores da própria internet estão disseminando o tempo todo; 100% de tudo o que você leu, ouviu, assistiu, etc., precisa de provas contundentes (referências lógicas válidas), para alcançar CVJV, caso contrária não terá validade.

Claude Shannon

Em 1948, publicou o importante artigo científico intitulado A Mathematical Theory of Communication July, October, 1948 – C. E. SHANNON enfocando o problema de qual é a melhor forma para codificar a informação que um emissor queira transmitir para um receptor.

Clique na foto de Shannon (Courtesy of MIT Museum) e baixe em PDF seu mais importante trabalho.

New Developments in Statistical Information Theory Based on Entropy and Divergence Measures – Leandro Pardo

Leitura recomendada para pesquisadores em estatística aplicada e medidas de divergências. Clica na capa do livro para iniciar a leitura.

O excelente vídeo baixo explica como extraímos informações usando matemática avançada

Sob apenas uma condição, um sinal amostrado pode ser perfeitamente recuperado. isso parece quase paradoxal, já que a amostragem de um sinal aparentemente remove quase todas as informações dele. Então, como isso é matematicamente possível? Qual é essa condição? Assista ao vídeo abaixo e saiba como!

A matemática é a linguagem com a qual escrevemos as partituras que representam uma aproximação da realidade (universo), cujo pano de fundo é a entropia, a origem do conhecimento é o vazio { } e a informação é a possibilidade existencial que pode ser particionada e compactada em espaços e subespaços.

{RC}.

Referências Bibliográficas

9 respostas em “Teoria da informação e entropia – como passamos do conhecimento para a informação?”

  1. Pingback: Saiba identificar PCE e PCI no campo da simulação cerebral – {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  2. Pingback: Qual a diferença entre Conhecimento, Informação e Dados? – Comece 2022 com essas dúvidas resolvidas! – {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  3. Pingback: Em que devemos acreditar? A resposta correta é: no grau de probabilidade dos existenciais! – {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  4. Pingback: O que é realidade? | {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  5. Pingback: O senso comum em confronto com nossa simulação biológica e cerebral | {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  6. Pingback: Como perceber PCI para alcançar PCE? | {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  7. Pingback: Tratamento do axioma C(∅) = 0 internalização do conhecimento | {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  8. Pingback: Tratamento do axioma μ(∅) – Razão instrumental | {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

  9. Pingback: Qual a origem do conhecimento? A resposta é a percepção do vazio ∅ | {RCRISTO – Matemática, Ciência, Tecnologia, Informação, Conhecimento}

Deixe um comentário

Este site utiliza o Akismet para reduzir spam. Saiba como seus dados em comentários são processados.