O que são espaços/subespaços probabilísticos?

Tanto na matemática quanto na física e principalmente na teoria da informação, aplicamos os conceitos de possibilidades/probabilidades junto com a adição do qualificativo existencial para completar o conceito de espaços e suas subdivisões: subespaços.
O conceito de probabilidade é considerado um conceito primitivo que não pode ser definido em termos de conceitos ainda mais primitivos, assim como um ponto ou uma linha na geometria são considerados conceitos primitivos. Deste modo, mesmo na falta de uma definição adequada do termo, probabilidade é um conceito fascinante e extremamente útil.
A teoria da probabilidade foi desenvolvida principalmente no século XVII por Fermat (1601-1665), Pascal (1623-1705), Huyghens (1629-1695) e por J. Bernoulli (1654-1705). A principal motivação para desenvolver a teoria matemática da probabilidade foi responder várias perguntas sobre jogos e aleatoriedade.
Abordagem Axiomática
Na matemática, um axioma é uma hipótese inicial por meio da qual outros enunciados são logicamente derivados. Pode ser uma sentença, uma proposição, um enunciado ou uma regra que permite a construção de um sistema formal. Diferentemente de teoremas, axiomas não podem ser derivados por princípios de dedução e não são demonstráveis por derivações formais, simplesmente porque já são hipóteses iniciais. Isto é, não há um predecessor lógico envolvido (caso contrário eles seriam chamados teoremas). Em muitos contextos, “axioma“, “postulado” e “hipótese” são usados como sinônimos.
Espaço de probabilidade
A abordagem axiomática da probabilidade foi desenvolvida principalmente por Kolmogorov na década de 1930 do século 20. Consiste nos três elementos denotados como {Ω, F, P}, que juntos definem o espaço de probabilidade. Os três elementos do espaço de probabilidade são os seguintes.
O espaço amostral Ω
Para descrever a incerteza, a probabilidade exige que se defina o conjunto de todos os resultados possíveis. Na teoria da probabilidade, este conjunto é muitas vezes chamado de espaço amostral e denotado pelo símbolo Ω (ômega), é o conjunto de todos os possíveis resultados de um experimento específico (às vezes chamado de tentativas). No contexto da teoria da probabilidade, subconjuntos são frequentemente chamados de eventos.
Obs: Espaço amostral é o conjunto de todos os possíveis resultados do experimento aleatório, denotado por Ω.
Ex1:
O espaço amostral de todos os resultados possíveis do lançamento de uma moeda consiste em dois elementos Ω = {H, T}, onde H representa cara e T representa coroa. O espaço amostral do lançamento de um dado consiste nos seis resultados possíveis Ω = {1, 2, 3, 4, 5, 6}. Estes são chamados de eventos simples ou “pontos” no espaço amostral. Na maioria dos casos, eventos simples são igualmente prováveis, neste caso, chamados de eventos elementares. Claramente, não podemos escrever o espaço amostral para cada experimento. Alguns consistem em um número infinito de elementos (por exemplo, atirar uma flecha em um alvo circular), alguns nem podem ser descritos (por exemplo, como será o mundo no próximo ano). Estaremos interessados apenas em espaços simples onde a contagem dos resultados referidos como eventos elementares é direta.
O campo de eventos F
Um evento composto, ou simplesmente um evento, é definido como uma união, ou uma soma de eventos elementares. Exemplos de eventos são:
(a) O resultado do lançamento de um dado é “par”; consiste nos eventos elementares {2, 4, 6}, ou seja: 2, 4 ou 6 ocorreram, ou ocorrerão no experimento de lançar um dado.
(b) O resultado do lançamento de um dado é “maior ou igual a 5”; consiste nos eventos elementares: {5, 6}, ou seja, 5 ou 6 ocorreram.
Em termos matemáticos, F consiste em todos os conjuntos parciais do espaço amostral Ω. Observe que o próprio evento Ω pertence a F. Além disso, o evento vazio denotado ∅ também pertence a F.
Discutiremos principalmente espaços amostrais finitos. Também aplicaremos alguns dos resultados a espaços infinitos ou mesmo contínuos usando argumentos de analogia. Um tratamento mais rigoroso requer as ferramentas da teoria da medida.
Para o espaço amostral finito, cada conjunto parcial de Ω é um evento. Se existem n eventos elementares em Ω, então o número total de eventos em F é 2n. Isso pode ser visto pela contagem direta:
um evento denotado por ∅ (o evento impossível ou vazio).
O símbolo significa
.
Por definição 0! = 1,
portanto .
eventos simples (ou elementares).
eventos que consistem em dois eventos simples.
eventos que consistem em três eventos simples.
um evento, consiste em todo o espaço Ω (o evento completo).
Ao todo, temos 2n eventos, ou seja:
Usamos o teorema do binômio de Newton para realizar a soma. Uma forma mais geral do teorema é:
Relação de Stifel
Em matemática, a relação de Stifel, também conhecida como regra de Pascal, é uma identidade envolvendo coeficientes binomiais:
Essa fórmula pode ser interpretada como: o número total de combinações de k objetos diferentes de n é denominado coeficiente binomial. A principal diferença entre permutações e combinações é a ordem. Combinações são seleções não ordenadas, permutações são arranjos ordenados. Para inteiros não negativos n e k com k ≤ n. A quantidade (pronuncia-se: n escolhe k) tem a interpretação: o número total de maneiras de escolher k objetos diferentes de n objetos distinguíveis – sem prestar atenção à sua ordem.
Um método alternativo para calcular o número total de eventos é o seguinte: representamos os eventos simples de Ω pelos números (1, 2, 3,…,n). Este é um vetor de n dimensões. Cada evento composto também pode ser descrito como um vetor de n dimensões. Por exemplo, o evento que consiste nos três eventos elementares (3, 5, 7) pode ser escrito como um vetor n-dimensional da forma: (Não, Não, Sim, Não, Sim, Não, Sim, Não, Não, . . . , Não), os componentes um e dois não estão inclusos, o componente três está incluso, quatro não está incluso, cinco está incluso e assim por diante.
Um evento composto é um conjunto parcial de Ω. Portanto, podemos descrever o evento composto simplesmente consultando a lista de eventos simples que estão inclusos nesse evento. Os componentes dos eventos compostos são Sim ou Não de acordo com a inclusão ou não de um evento simples específico. Assim, cada evento pode ser escrito de forma única como um vetor n-dimensional que consiste em Sim(s) e Não(s) ou “1” e “0“. Claramente, como o comprimento do vetor é n, e cada componente pode ser “Sim” ou “Não”, juntos temos 2n desses vetores correspondentes a todos os eventos compostos possíveis. Nesta notação, o evento impossível é escrito como: (não, não, não). E o evento certo como: (sim, sim, sim).
Nesta fase, introduzimos algumas notações sobre operações entre eventos.
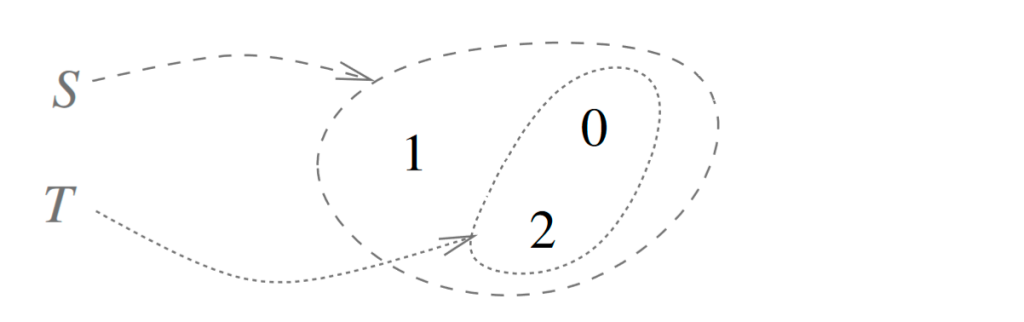
O evento A ∪ B (ou A, B) é chamado de união (ou soma) dos dois eventos. Este é o evento: “ou ocorreu A ou B”. O evento A ∩ B (ou A · B) é chamado de interseção (ou produto) dos dois eventos. Este é o evento: “A e B ocorreram”.
O evento complementar, denotado (ou Ω − A), é o evento: “A não ocorreu”.
A notação A ⊂ B significa: A é parcial a B, ou A está incluso no evento B, a ocorrência de A implica a ocorrência de B.
Essas relações entre eventos estão descritas na Figura 2.

A função de probabilidade representada por P
Para cada evento A pertencente a F, atribuímos um número P chamado probabilidade do evento A. Este número atende ao seguinte:
a: P(Ω) = 1,
b: 0 ≤ P(A) ≤ 1,
c: Se A e B são eventos disjuntos (ou mutuamente excludentes), então P(A ∪ B) = P(A) + P(B).
As duas primeiras condições definem o intervalo de números para a função de probabilidade. A primeira condição significa simplesmente que o evento Ω tem o maior valor de probabilidade. Por definição, assumimos que algum resultado ocorreu, ou ocorrerá, portanto, o evento Ω também é referido como o evento certo, e é atribuído o valor de 1. O evento impossível, denotado ∅, recebe o número zero, ou seja, P(∅) = 0 (uma probabilidade vazia é igual a 0).
A terceira condição é intuitivamente clara. Dois eventos A e B são ditos disjuntos, ou mutuamente exclusivos (ou excludentes), quando a ocorrência de um evento exclui a possibilidade da ocorrência do outro. Em termos matemáticos dizemos que a interseção de dois eventos (A ∩ B) é vazia = ∅; ou seja, não existe evento simples que seja comum a ambos A e B.
Como exemplo simples, considere dois eventos:
A = {o resultado do lançamento de um dado é par},
B = {o resultado do lançamento de um dado é ímpar}.
Claramente, os eventos A e B são disjuntos, a ocorrência de um exclui a ocorrência do outro.
Agora, defina o evento:
C = {o resultado do lançamento de um dado é maior ou igual a 5}.
Claramente, A e C, ou B e C não são disjuntos. A e C contêm o evento elementar 6. B e C contêm o evento elementar 5. Os eventos “maior ou igual a 4” e “menor ou igual a 2” são eventos claramente disjuntos ou mutuamente exclusivos. Antecipando a discussão acima, podemos calcular a probabilidade do primeiro evento {4, 5, 6} ser 3, se os dois eventos não forem disjuntos, digamos “maior ou igual a 4” e “par”, então a regra (c) deve ser modificada, isso pode ser comprovado pelas propriedades listadas em:D = P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
Probabilidade da união de dois eventos
A probabilidade da união de dois eventos, A e B, é calculada pela probabilidade do evento A ocorrer, mais a probabilidade do evento B ocorrer, menos a interseção entre A e B.
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Portanto, a probabilidade da união de dois eventos é igual à soma da probabilidade de cada um desses eventos ocorrerem menos a interseção entre os dois. Quando os eventos são mutuamente excludentes, ou seja, a interseção entre eles é vazia, então a probabilidade da união é a soma das probabilidades de ocorrências de cada um deles.
P(A ∪ B) = P(A) + P(B)
Como calcular a probabilidade da união de dois eventos?
Ex2:
Numa sala de aula, há 30 alunos, sendo que 20 são meninas e 10 meninos. Durante as aulas de matemática, o professor resolveu fazer um sorteio entre os alunos que se saíram melhor no teste. Sabendo que nessa sala 10 alunos usam camisetas brancas e que 5 deles são meninas, calcule a probabilidade de o sorteado ser uma menina ou alguém que usa camiseta branca. Para calcular a probabilidade da união de dois conjuntos é necessário encontrar os dados para calcular cada uma das probabilidades. São eles:
n(A) → número de elementos correspondentes ao evento A;
n(B) → número de elementos correspondentes ao evento B;
n(Ω) → número de elementos no espaço amostral;
n(A ∩ B) → número de elementos na interseção entre os eventos A e B.
Fazendo essa substituição:
n(A) é igual ao número de meninas.
n(A) = 20
n(B) é igual ao número de alunos que usam camisetas brancas.
n(B) = 10
n(Ω) → número de alunos.
n(Ω) = 30
n(A ∩ B) → número de meninas que usam camisas brancas.
n(A ∩ B) = 5
Então, temos que:
Muito cuidado com a Interseção

Representação gráfica da interseção entre dois conjuntos.
Na teoria dos conjuntos, a interseção é um conjunto de elementos que, simultaneamente, pertencem a dois ou mais conjuntos, representado por ∩ (símbolo de Interseção).
Por exemplo, se o conjunto A possui os elementos {1,2,3,4,5} e o conjunto B possui os elementos {2,4,6,8}, então a interseção do conjunto A com o conjunto B será igual a {2,4}.
Definição
Na teoria básica dos conjuntos, define-se A ∩ B por:
A ∩ B = {x|x ∈ A ∧ x ∈ B}
Lê-se: a interseção entre os conjuntos A e B é igual ao espaço x tal que x pertence ao conjunto A e x pertence ao conjunto B.
Pelos axiomas de Zermelo-Fraenkel, a definição acima não é válida. Devemos usar o axioma da separação com a fórmula Φ = x ∈ w:
∀z∀w∃y∀x(x ∈ y ⟺ ( x ∈ z ∧ x ∈ w))
Esse axioma garante a existência da interseção (y = z ∩ w) o enunciado do axioma da separação é tal que, usando-se o axioma da extensão, pode-se mostrar que y é único.
Em outras palavras, provou-se que:
∀A∀B∃!(A ∩ B) ∀ x(x ∈ (A ∩ B) ⟺ (x ∈ A ∧ x ∈ B ))
Lê-se: para todo A, para todo B, existe exatamente uma interseção entre A e B, para todo x, x pertence à interseção entre A e B, se e somente se o espaço x pertence a A e x pertence a B.
Obs: em notação matemática você não pode ter nenhuma dúvida, caso você observe um símbolo qualquer e não identifique o sentido desse símbolo, procure imediatamente o significado desse símbolo ou notação, caso contrário, não poderá continuar os estudos e a dúvida acompanhará você.
Propriedades
Considerando-se que (x ∈ A ∧ x ∈ B) ⟺ (x ∈ B ∧ x ∈ A) e que ((x ∈ A ∧ x ∈ B) ∧ x ∈ C) ⟺ (x ∈ A ∧ (x ∈ B ∧ x ∈ C)), prova-se que:
∀A∀B(A ∩ B = B ∩ A)
∀A∀B∀C((A ∩ B) ∩ C = A ∩ (B ∩ C))
Como o conjunto vazio ∅ tem a propriedade que ∀x (x ∉ ∅), temos que:
∀A(A ∩ ∅ = ∅)
Deve-se tomar cuidado ao dizer que ∩ é associativa e comutativa, porque – a rigor – associatividade e comutatividade são propriedades de operações binárias, e a interseção foi definida para todos os conjuntos – tratar todos os conjuntos como um conjunto gera paradoxos.
Interseções arbitrárias
Seja M uma coleção não-vazia de conjuntos (em teoria dos conjuntos na sua formulação segundo os axiomas de Zermelo-Fraenkel, todo conjunto tem como elementos outros conjuntos, então basta dizer que M não é vazio). Então podemos definir a interseção de todos os conjuntos de M:
como sendo o conjunto cujos elementos x são elementos de todos os elementos de M:
O problema é que essa definição não é rigorosa, mas isso pode ser resolvido usando-se o axioma da união:
.
O conjunto vazio ∅ como núcleo existencial
É derivado do Axioma do Infinito na teoria dos conjuntos e torna-se o elemento primordial de todos os espaços e subespaços que nascem vazios. Para conhecer em profundidade sugiro a leitura técnica: Matemática do vazio – Resolva equívocos e pense com clareza!
Obs: na teoria dos conjuntos, os membros do conjunto são os próprios conjuntos, é diferente da matemática usual do cotidiano, cujos objetos são usados e geralmente representados de forma isolada.
Prova da árvore de subconjuntos ∅ ⊆ ∅

Dado um número n = 0, temos 20 = 1 subconjuntos. O único conjunto com zero elementos é o conjunto vazio que só tem um subconjunto: ele próprio, portanto, a propriedade é verdadeira para n = 0.
P: 2Ω → [0, 1]
P(ωi) = n(ωi)/N(Ω) = número de elementos em ωi/número de elementos no espaço amostral Ω.
Em qualquer problema de probabilidade, é muito importante identificar todos os diferentes resultados que podem ocorrer. Portanto, o ponto de partida é o espaço amostral (probabilidades), ou seja, um conjunto de todos os resultados possíveis. É denotado geralmente como Ω. Para o conjunto Ω = (ω1, ω2,…), uma probabilidade é uma função de valor real P definida nos subespaços de Ω:
P: 2Ω → [0, 1]
O conjunto de todos os resultados possíveis de um experimento de probabilidade é chamado de espaço amostral. Se Ω é o espaço amostral, então a probabilidade de ocorrência de um evento ωi é definida como:
P(ωi) = n(ωi)/N(Ω) = número de elementos em ωi/número de elementos no espaço amostral Ω.
Os valores da função P(ωi) são considerados como probabilidades de eventos elementares ωi. A função P(ωi) satisfaz a condição de normalização P(ωi) = 1. A probabilidade de um evento A pode ser escrita como P(A), p(A) ou Pr(A). Essa definição matemática de probabilidade pode se estender a espaços amostrais infinitos e até mesmo a espaços amostrais incontáveis, usando o conceito de medida.
Para prosseguir, deve-se exigir que a função P seja não-negativa e que seus valores nunca excedam 1. Os subespaços de Ω para os quais P é definido são chamados de eventos. Eventos de elemento único são chamados de eventos elementares que consistem em mais de um resultado e são chamados de eventos compostos. Qualquer subconjunto do espaço amostral é um evento. Os conjuntos A ⊂ Ω são chamados por eventos e suas probabilidades são definidas por:
P(A) = ∫p(ωi)/ωi ⊂ A
A função P deve ser definida no subespaço vazio ∅ e em todo o conjunto Ω:
P (∅) = 0, P (Ω) = 1
Esta afirmação enfatiza em particular que tanto ∅ quanto Ω são eventos. O evento ∅ que nunca acontece é impossível e tem probabilidade 0. O evento Ω tem probabilidade 1, é certo ou necessário.
Demonstração:
Seja P(A) o conjunto de partes de A e n(S) o número de elementos distintos de S.
Se A = ∅ → P(A) = {∅} → n(P(A)) = 2^0 = 1
Se A = {a} → P(A) = {∅,a} → n(P(A)) = 2^1 = 2
Se A = {a,b} → P(A) = {∅,a,b,{a,b} → n(P(A)) = 2^2 = 4
Se A = {a,b,c} → P(A) = {∅,a,b,c,{a,b},{b,c},{a,c},{a,b,c}} → n(P(A)) = 2^3 = 8
P(A) é formado por ∅ somado às possíveis combinações dos elementos de A, com taxa variando de 1 a n(A). Assim, n(P(A)) = número de combinações n(A), com taxa variando de 1 a n(A) somado a 1 (responsável por ∅).
Se A = ∅, o número de elementos de P(A) = 1, pois P(A) = {∅}, então n[P(A)] = 1, também ; portanto, n(A) = 0, cujo resultado: n[P(A)] = 20 = 1.
Explicação não formal sobre as potências vazias
Para um conjunto vazio A, o conjunto de potências P(A) consiste em apenas um elemento, o conjunto vazio.
Isso ocorre porque um conjunto de potências é definido como o conjunto de todos os subconjuntos de um conjunto dado. Se A não contém elementos, não há subconjuntos possíveis, exceto o próprio conjunto vazio.

Recomendo a leitura do livro (clique na capa para ler): Linear Algebra Done Right – Four Edition 2023 – Sheldon Axler. Tanto Sheldon quanto eu, somos extremamente detalhistas em relação ao estudo da matemática, nenhuma dúvida pode ficar sem respostas. Segue abaixo nota do autor. {RC}.
Você provavelmente está prestes a começar sua segunda exposição à álgebra linear. Diferente de seu primeiro contato com o assunto, que provavelmente enfatizou os espaços euclidianos e matrizes, este encontro se concentrará em espaços vetoriais abstratos e mapas lineares. Esses termos serão definidos posteriormente, então não se preocupe se você não souber o que eles querem dizer. Este livro começa desde o início do assunto, assumindo nenhum conhecimento de álgebra linear. O ponto chave é que você está prestes a mergulhar na matemática séria, com ênfase em atingir uma compreensão profunda das definições, teoremas e provas.
Você não pode ler matemática da mesma forma que lê um romance. Se você passar por uma página em menos de uma hora, provavelmente está indo rápido demais. Quando você encontra a frase “você deve verificar”, você deve realmente fazer a verificação, que geralmente exigirá alguma escrita de sua parte. Quando as etapas são omitidas, você precisa fornecer as peças que faltam. Você deve ponderar e internalizar cada definição. Para cada teorema, você deve buscar exemplos para mostrar por que cada hipótese é necessária. Discussões com outros alunos devem ajudar.
Como auxílio visual, as definições estão em caixas bege e os teoremas estão em caixas azuis (em versões coloridas do livro). Cada teorema tem um nome descritivo.
Por favor, verifique o site abaixo para obter informações adicionais sobre o livro. Posso ocasionalmente escrever novas seções sobre tópicos adicionais. Essas novas seções serão postadas no site. Suas sugestões, comentários e correções são muito bem-vindas.
Muitas felicidades, sucesso e prazer em aprender álgebra linear!
- Sheldon Axler
- Mathematics Department
- San Francisco State University
- San Francisco, CA 94132, USA
- website: linear.axler.net
- e-mail: linear@axler.net
- Twitter: @AxlerLinear
Exemplo de visualização de um espaço de probabilidade com seus subespaços internos
Uma medida de probabilidade sobre uma σ-álgebra (lê-se Sigma Álgebra) F ⊂ 2 Ω, associada a um espaço amostral Ω, é uma função P : F → [0, 1] tal que:
- P(∅) = 0
- P(Ω) = 1
- se A ∩ B = ∅, A, B ∈ F então P(A ∪ B) = P(A) P(B) (aditividade).
Um espaço amostral Ω junto com uma σ-álgebra F com seus subespaços e uma medida de probabilidade P em F forma um espaço de probabilidade, ou seja, o tripleto (Ω, F, P). Com base na noção de espaço de probabilidade, pode-se definir a noção de uma variável aleatória. Uma variável aleatória é uma quantidade cujo valor está sujeito a variações aleatórias, ou seja, ao “acaso”. Obs: segue um exemplo prático de variáveis aleatórias desenvolvido em Java neste poste: O senso comum em confronto com nossa simulação biológica e cerebral.
No experimento da Figura 5, as tentativas de girar a roda levam a um evento subconjunto (subespaço) do espaço amostral Ω; no tempo decorrido de repetidas tentativas, cada evento tende a ocorrer com uma taxa persistente, esta taxa é chamada de “frequência relativa”.
Subespaços lineares
Referências Bibliográficas
- O senso comum em confronto com nossa simulação biológica e cerebral
- Wikipedia matemática
- Probabilidade da união de dois eventos
- Interseção
- Probabilidade e Estatística – Quantificando A Incerteza – Joao Pinheiro, Sonia Cunha, Gastão Gomes, Santiago Carvajal
- Estatística Básica – A arte de trabalhar com dados – Sergio Albuquerque
- Probabilidade e Estatística – Francisco de Assis Amaral Bastos
- Introduction to Real Analysis, Volume I November 9, 2021 (version 5.5) – Jiri Lebl
- Sheldon Axler
- Linear Algebra Done Right – Four Edition 2023 – Sheldon Axler
- The Geometry of Uncertainty The Geometry of Imprecise Probabilities – Fabio Cuzzolin
- Khan Academy